Introduction to Tree, Binary Tree And Expression Tree
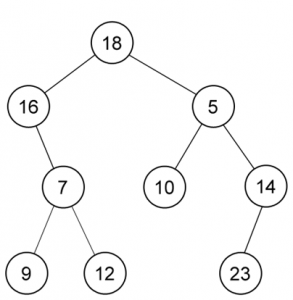
Tree adalah sebuah data struktur yang terdiri dari kumpulan node.
–> Node teratas disebut root.
–> Node dibawahnya disebut child.
–> Node yang tidak memiliki child disebut leaf.
–> Degree : Total sub-tree dari node yang ada.
–> Height : Maksimum degree dari sebuah tree.
Binary Tree : sebuah data struktur yang maksimum memiliki 2 buah node. Kedua node tersebut bisa dianggap sebagai left dan right child.
Tipe-Tipe Binary Tree :
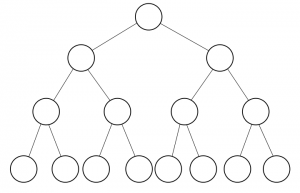
1. Perfect Binary Tree : Binary Tree yang tiap node mempunyai 2 child dan berada pada level yang sama.
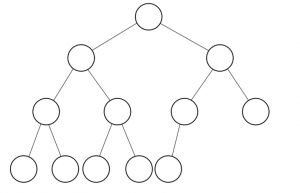
2. Complete Binary Tree : Binary tree yang tiap level terisi oleh node kecuali yang paling kiri dan semua node di buat sekiri mungkin. Perfect Binary Tree adalah sebuah Complete Binary Tree.
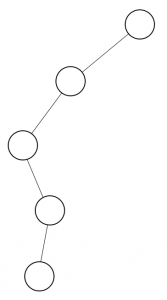
3. Skewed Binary Tree : Binary tree yang tiap level hanya mempunyai 1 child.
Properti dari Binary Tree:
- Jumlah maksimal node pada binary tree dari level k adalah 2<sup>K</sup>
- Jumlah maksimal node pada binary tree dari height h adalah 2<sup>h+1</sup>-1
- Height maksimum suatu binary tree dari node n adalah <sup>2</sup>log(n)
- Height minimum suatu binary tree dari node n adalah n-1
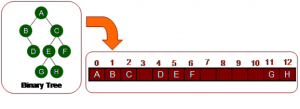
Representasi dari Binary Tree menggunakan Array
- Index dari array merepresentasikan atau menunjukan nomor node.
- Index ke-0 merupakan root.
- Index dari Left Child adalah 2p + 1, dimana p = index dari parent.
- Index dari Right Child adalah 2p + 2, dimana p = index dari parent.
- Index dari Parent adalah (p-1)/2.
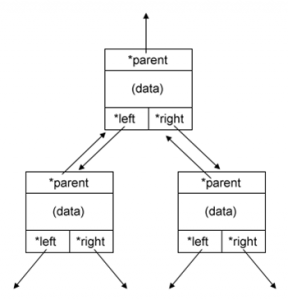
Representasi dari Binary Tree menggunakan Linked List
Expression Tree :
–> Expression Tree dapat dibuat dari prefix atau postfix dengan proses rekursif.
Konsep dari expression tree:
- Prefix : Print L R
Contoh : *+abc - Postfix : L R Print
Contoh : ab+c* - Infix : L Print R
Contoh : (a+b)*c